星までの距離はどうやって測るの？
皆さんは、理科の教科書などで○○星まで△△光年といった表記を見たことはないでしょうか。例えばおおいぬ座のシリウスは8.6光年、我々の住む太陽系が属する天の川銀河の外側にあるアンドロメダ銀河は230万光年先にあります。つまり、光の速さで向かっても230万年もかかるほど遠くにあるのです。
距離の測り方
ところで、こんなに遠くにある星々までの距離をどのようにして測っているのでしょうか。私たちが長さを測るときに使うメジャーなどはとても使えません。また、私たちは星空を眺めてみてもどの星が近く、どの星が遠いのかも分かりません。そこで天文学では年周視差を用いて距離を測っています。
年周視差とは？
地球は太陽の周りを公転しています。この公転軌道の直径を三角形の一辺として、今の地球、半年前の地球、星で二等辺三角形を作ります。この二等辺三角形の頂角の半分を年周視差Pといいます。年周視差は望遠鏡を使って計測することができます。この年周視差と三角比を使って星の距離を求めるのです。
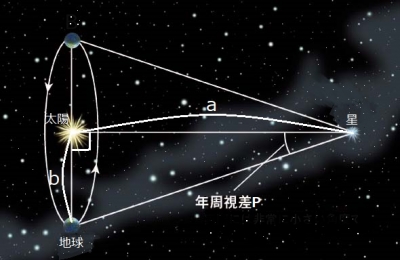年周視差の図
Image Credit : NAOJ
あのtanが使える！
二等辺三角形を半分にして直角三角形に注目してみましょう。この直角三角形のうち年周視差であるPと太陽と地球の距離bは観測からわかっています。直角三角形の二辺の比はtanで表せます。つまり
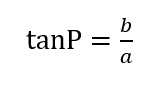
です。皆さん、数学の教科書の1番最後のページにある三角関数表を見てみてください。この表にはそれぞれの角度に相当するtanの値が書かれています。上の式にPとbの値を代入すると、星までの距離であるaが求まりますね。高校で習うときはどこで使われているのか想像がつかない三角比はこういったところで使われているのです。
星の距離を測ることの限界
年周視差は、星の距離を直接的に測れる唯一の方法ですが、問題点もあります。実は年周視差は一番近い星でも1°の4800分の1と極めて小さいため、せいぜい1500光年ほどの距離までしか測れません。それよりもっと遠くの星は、年周視差で距離のわかっている星からヒントを得て、様々なアプローチから間接的に求めています。
